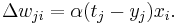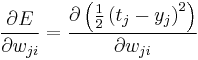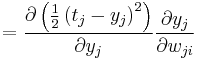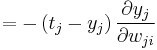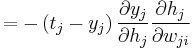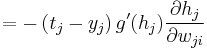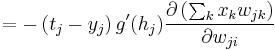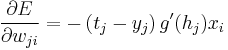Delta rule
The delta rule is a gradient descent learning rule for updating the weights of the artificial neurons in a single-layer perceptron. It is a special case of the more general backpropagation algorithm. For a neuron 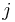 with activation function
with activation function 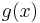 the delta rule for
the delta rule for 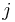 's
's 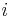 th weight
th weight 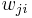 is given by
is given by
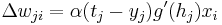 ,
,
where
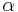 is a small constant called learning rate is a small constant called learning rate |
|
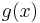 is the neuron's activation function is the neuron's activation function |
|
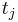 is the target output is the target output |
|
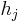 is the weighted sum of the neuron's inputs is the weighted sum of the neuron's inputs |
|
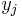 is the actual output is the actual output |
|
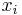 is the is the 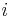 th input. th input. |
It holds that 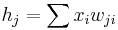 and
and 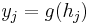 .
.
The delta rule is commonly stated in simplified form for a perceptron with a linear activation function as
Derivation of the delta rule
The delta rule is derived by attempting to minimize the error in the output of the perceptron through gradient descent. The error for a perceptron with 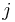 outputs can be measured as
outputs can be measured as
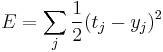 .
.
In this case, we wish to move through "weight space" of the neuron (the space of all possible values of all of the neuron's weights) in proportion to the gradient of the error function with respect to each weight. In order to do that, we calculate the partial derivative of the error with respect to each weight. For the 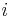 th weight, this derivative can be written as
th weight, this derivative can be written as
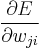 .
.
Because we are only concerning ourselves with the 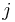 th neuron, we can substitute the error formula above while omitting the summation:
th neuron, we can substitute the error formula above while omitting the summation:
Next we use the chain rule to split this into two derivatives:
To find the left derivative, we simply apply the general power rule:
To find the right derivative, we again apply the chain rule, this time differentiating with respect to the total input to 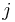 ,
, 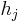 :
:
Note that the output of the neuron 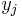 is just the neuron's activation function
is just the neuron's activation function 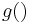 applied to the neuron's input
applied to the neuron's input 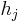 . We can therefore write the derivative of
. We can therefore write the derivative of 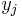 with respect to
with respect to 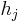 simply as
simply as 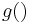 's first derivative:
's first derivative:
Next we rewrite 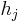 in the last term as the sum over all
in the last term as the sum over all 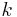 weights of each weight
weights of each weight 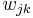 times its corresponding input
times its corresponding input 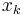 :
:
Because we are only concerned with the 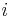 th weight, the only term of the summation that is relevant is
th weight, the only term of the summation that is relevant is 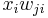 . Clearly,
. Clearly,
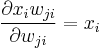 ,
,
giving us our final equation for the gradient:
As noted above, gradient descent tells us that our change for each weight should be proportional to the gradient. Choosing a proportionality constant 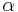 and eliminating the minus sign to enable us to move the weight in the negative direction of the gradient to minimize error, we arrive at our target equation:
and eliminating the minus sign to enable us to move the weight in the negative direction of the gradient to minimize error, we arrive at our target equation:
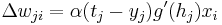 .
.